Китайская теорема об остатках

Ссылки [ править ]

Dauben, Joseph W. (2007), «Глава 3: Китайская математика», в Katz, Victor J. (ed.), The Mathematics of Egypt, Mesopotamia, China, India and Islam: A Sourcebook , Princeton University Press, стр. 187–384, ISBN 978-0-691-11485-9
Денс, Джозеф Б .; Денс, Томас П. (1999), Элементы теории чисел , Academic Press, ISBN 9780122091308
Duchet, Pierre (1995), «Hypergraphs», в Graham, RL; Grötschel, M .; Ловас, Л. (ред.), Справочник по комбинаторике, Vol. 1, 2 , Амстердам: Elsevier, стр. 381–432, MR 1373663. См., В частности, раздел 2.5 «Свойство Хелли», стр. 393–394 .
Гаусс, Карл Фридрих (1986), Disquisitiones Arithemeticae , переведенный Кларком, Артуром А. (Второе, исправленное изд.), Нью-Йорк: Springer , ISBN 978-0-387-96254-2
Ирландия, Кеннет; Розен, Майкл (1990), Классическое введение в современную теорию чисел (2-е изд.), Springer-Verlag, ISBN 0-387-97329-X
Как, Субхаш (1986), «Вычислительные аспекты алгоритма Арьябхата» , Индийский журнал истории науки , 21 (1): 62–71
Кац, Виктор Дж. (1998), История математики / Введение (2-е изд.), Аддисон Уэсли Лонгман, ISBN 978-0-321-01618-8
Либбрехт, Ульрих (1973), Китайская математика в тринадцатом веке: «Шу-шу Чиу-чан» Цинь Цзю-шао , Dover Publications Inc, ISBN 978-0-486-44619-6
Оре, Ойстейн (1988) , Теория чисел и ее история , Дувр, ISBN 978-0-486-65620-5
Пизано, Леонардо (2002), Liber Abaci Фибоначчи , переведенная Сиглером, Лоуренсом Э., Springer-Verlag, стр. 402–403, ISBN 0-387-95419-8
Розен, Кеннет Х. (1993), Элементарная теория чисел и ее приложения (3-е изд.), Addison-Wesley, ISBN 978-0201-57889-8
Сенгупта, Амбар Н. (2012), Представление конечных групп, Полупростое введение , Springer, ISBN 978-1-4614-1232-8

Операция «Раздолбай»

На главную
Задачи в Корявове
Лекции
Гуманитарные курсы
Английский язык
▼ 1 семестр
Аналитическая геометрия
Общая физика
Мат.Анализ (+коллоквиум)
История
▼ 2 семестр
Линейная алгебра
Мат.Анализ
Общая физика
▼ 3 семестр
Мат.Анализ
Лабы по общ.физу
Общая физика
Теоретическая механика
▼ 4 семестр
Мат.Анализ
Лабы по общ.физу
Общая физика
Дифф. уравнения
Теоретическая механика
▼ 5 семестр
Компьютерные сети
Теоретическая физика
ТФКП
Общая физика (ГОС)
▼ 6 семестр
Уравнения мат.физики
Мат.Анализ (ГОС)
▼ 7 семестр
Защита информации
Теоретическая физика
▼ 8 семестр
▼ 9+ семестры
Испанский язык
Философия (асп)

Если натуральные числа попарно взаимно просты, то

Более того, если найдутся два таких числа и , то

Доказательство

Воспользуемся методом математической индукции.

При утверждение теоремы очевидно.

Пусть теорема справедлива при , т.е. существует число , дающее остаток при делении на при .

Обозначим . И рассмотрим числа

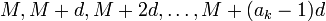Покажем, что хотя бы одно из этих чисел дает остаток при делении на . Допустим это не так. Поскольку количество чисел равно , а возможных остатков при делении этих чисел на может быть не более чем , то среди них найдутся два разных числа, имеющих равные остатки. Пусть это числа и при и . Тогда их разность должна делиться на , что невозможно, приходим к противоречию.

Применения

Китайская теорема об остатках широко применяется в теории чисел, криптографии и других дисциплинах.

Взаимно однозначное соответствие между некоторым числом и набором его остатков, определяемым набором взаимно простых чисел, существование которого утверждается в теореме, на практике помогает работать не с длинными числами, а с наборами их коротких по длине остатков. Кроме того вычисления по каждому из модулей можно выполнять параллельно. . Если в качестве базиса взять к примеру первые 500 простых чисел, длина каждого из которых не превосходит 12 бит, то этого хватит для представления десятичных чисел длины 1519 знаков. (Откуда взялось число 1519 понять очень просто: сумма десятичных логарифмов первых 500 простых чисел есть 1519.746…).

Например, в алгоритме RSA вычисления производятся по модулю очень большого числа n, представимого в виде произведения двух больших простых чисел. КТО позволяет перейти к вычислениям по модулю этих простых делителей которые по величине уже порядка корня из n, а значит имеют в два раза меньшую битовую длину.

Отметим также, что применение вычислений согласно КТО делает алгоритм RSA восприимчивым к атакам по времени

На теореме основаны Схема Асмута — Блума и Схема Миньотта пороговые схемы разделения секрета в группе участников — секрет могут узнать только k из n участников объединив свои ключи.
Одним из применения является быстрое преобразование Фурье на основе простых чисел
Теорема лежит в основе принципа Хассе поиска целочисленных корней уравнения.
Из теоремы следует мультипликативность функции Эйлера.
На теореме основывается Алгоритм Полига — Хеллмана нахождения дискретного логарифма за полиномиальное время для чисел имеющих специальный вид.
Теорема имеет множество применений в шифровании и дешифровании в криптографических системах, например, в криптосистеме Рабина или в шифре Виженера.

Целочисленная система сравнения

Теорема

Пусть ,…, будут целыми числами два или два, которые предшествуют друг другу , то есть НОД ( n _i , n _j ) = 1, когда i ≠ j . Тогда для всех целых чисел … ,, существует целое число , единственное по модулю , такое, что
нет1{\ displaystyle n_ {1}}нетk{\ displaystyle n_ {k}}в1{\ displaystyle a_ {1}}вk{\ displaystyle a_ {k}}Икс{\ displaystyle x} нетзнак равно∏язнак равно1kнетя{\ Displaystyle п = \ прод _ {я = 1} ^ {к} п_ {я}}

Икс≡в1(моднет1)…Икс≡вk(моднетk){\ displaystyle {\ begin {matrix} x \ Equiv a_ {1} {\ pmod {n_ {1}}} \\\ ldots \\ x \ Equiv a_ {k} {\ pmod {n_ {k}}} \ \\ конец {матрица}}}

Алгоритм

Решение можно найти следующим образом. Для каждого i целые числа и взаимно просты. Согласно теореме Баше-Безу мы можем вычислить обратное по модулю . Для этого мы можем использовать расширенный алгоритм Евклида и получить целые числа и такие, что . Если мы позируем , то у нас есть
Икс{\ displaystyle x}нетя{\ displaystyle n_ {i}}нет^язнак равнонетнетязнак равнонет1…нетя-1нетя+1…нетk{\ displaystyle {\ hat {n}} _ {i} = {\ frac {n} {n_ {i}}} = n_ {1} \ ldots n_ {i-1} n_ {i + 1} \ ldots n_ {k}}vя{\ displaystyle v_ {i} \,}нет^я{\ Displaystyle {\ шляпа {п}} _ {я}}нетя{\ displaystyle n_ {i}}тыя{\ Displaystyle и_ {я} \,}vя{\ displaystyle v_ {i} \,}тыянетя+vянет^язнак равно1{\ displaystyle u_ {i} n_ {i} + v_ {i} {\ hat {n}} _ {i} = 1}еязнак равноvянет^я{\ displaystyle e_ {i} = v_ {i} {\ hat {n}} _ {i}}

ея≡1(моднетя){\ Displaystyle е_ {я} \ эквив 1 {\ pmod {п_ {я}}} \,}и для j ≠ i .ея≡(моднетj){\ Displaystyle е_ {я} \ эквив 0 {\ pmod {n_ {j}}} \,}

Таким образом, частным решением этой системы сравнения является

Иксзнак равно∑язнак равно1kвяея ,{\ displaystyle x = \ sum _ {i = 1} ^ {k} a_ {i} e_ {i} ~,}

а другие решения представляют собой целые числа, совпадающие по модулю произведения .
Икс{\ displaystyle x}нет{\ displaystyle n}

Пример

Пример Сунь Цзы, представленный ранее в разделе истории, сводится к

Икс≡2(мод3){\ Displaystyle х \ экв 2 {\ pmod {3}} \,}

Икс≡3(мод5){\ Displaystyle х \ эквив 3 {\ pmod {5}} \,}

Икс≡2(мод7){\ Displaystyle х \ эквив 2 {\ pmod {7}} \,}

тогда мы получаем

нетзнак равно3×5×7знак равно105{\ Displaystyle п = 3 \ раз 5 \ раз 7 = 105}
нет1знак равно3{\ displaystyle {n_ {1}} = 3}и , или такнет^1знак равно35 год{\ displaystyle {\ hat {n}} _ {1} = 35}2нет^1≡1(мод3){\ Displaystyle 2 {\ шляпа {п}} _ {1} \ Equiv 1 {\ pmod {3}}}е1знак равно70{\ displaystyle e_ {1} = 70}
нет2знак равно5{\ displaystyle n_ {2} = 5}и , или такнет^2знак равно21 год{\ displaystyle {\ hat {n}} _ {2} = 21}нет^2≡1(мод5){\ Displaystyle {\ шляпа {п}} _ {2} \ эквив 1 {\ pmod {5}}}е2знак равно21 год{\ displaystyle e_ {2} = 21}
нет3знак равно7{\ displaystyle n_ {3} = 7}и , или такнет^3знак равно15{\ displaystyle {\ hat {n}} _ {3} = 15}нет^3≡1(мод7){\ Displaystyle {\ шляпа {п}} _ {3} \ эквив 1 {\ pmod {7}}}е3знак равно15{\ displaystyle e_ {3} = 15}

решение для x тогдаИксзнак равно2×70+3×21 год+2×15знак равно233{\ Displaystyle х = 2 \ раз 70 + 3 \ раз 21 + 2 \ раз 15 = 233}

и все решения представляют собой целые числа, сравнимые с 233 по модулю 105, то есть 23 по модулю 105.

Обобщение на непростые числа

Системы сравнения могут быть решены, даже если n _i не простое между ними два на два. Точный критерий таков:

Пример: система x ≡ –1 mod 4 и x ≡ –1 mod 6 эквивалентна: x + 1, кратному 4 и 6, то есть PPCM (4, 6) = 12, или еще раз: x ≡ — 1 мод 12.

Одним из методов решения таких систем является , который заключается в сведении к простому модулю между ними два на два (в приведенном выше примере: модули 4 и 3). Другой — .

Механическая интерпретация

Решение системы  , из неизвестного , проходит мимо расчета PPCM из и .
{Икс≡р(модв)Икс≡s(модб){\ displaystyle \ left \ {{\ begin {array} {l} x \ Equiv r {\ pmod {a}} \\ x \ Equiv s {\ pmod {b}} \ end {array}} \ right.} Икс{\ displaystyle x}в{\ displaystyle a}б{\ displaystyle b}

Зубчатое колесо с зубьями входит в зацепление с другим зубчатым колесом, содержащим его зубья. Сколько зубов должно пройти, чтобы его -й зуб совпал с -м зубом?
в{\ displaystyle a}б{\ displaystyle b}р{\ displaystyle r}s{\ displaystyle s}

Для этой передачи , PPCM (12,15) = 60, для x ∈ решение x = 34.
{Икс≡4 (моd 15)Икс≡10 (моd 12){\ Displaystyle \ left \ {{\ begin {array} {l} x \ Equiv 4 ~ (mod ~ 15) \\ x \ Equ 10 ~ (mod ~ 12) \ end {array}} \ right.}

Мы можем легко понять, почему расчет на зубчатых колесах включает в себя модульную арифметику, отметив, что набор зубьев колеса путем подсчета n может быть параметризован набором корней n -й степени единицы , которая имеет групповую структуру, которая, естественно, изоморфна ℤ / n ℤ .

Сочетательный закон сложения

Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.

Сочетательный закон сложения: два способа

Результат сложения нескольких слагаемых не зависит от порядка действий.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.

Рассмотрим сумму из трех слагаемых:

1 + 3 + 4

Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:

1 + 3 + 4 = (1 + 3) + 4 = 5 + 4 = 8

Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:

1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8

В обоих случаях получается один и тот же результат — что и требовалось доказать.

Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:

(1 + 3) + 4 = 1 + (3 + 4)
8 = 8

Отразим сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Формула сочетательного закона для обыкновенных дробей:

Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.

Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.

Значит, сочетательный закон справедлив и для обыкновенных дробей.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Юрист Пьер де Ферма – «король среди любителей математики»

Пьер де Ферма (1601-1665) – французский судья и самоучка, известен как автор самой сложной теоремы всех времен. Свою карьеру и жизненный путь Ферма связал с юриспруденцией, и работал в местном парламенте маленького городка Кастр (до 1789 года «парламентом» во Франции называли суды).

Помимо блестящей карьеры в суде, Пьер также увлекался математикой, был самоучкой, черпая свои знания из книг и переписки со своими сверстниками, учеными и философами того времени – Декартом, Паскалем, Бернардом де Бесси и другими. Несмотря на его статус любителя, профессиональные математики ценили переписку с Пьером Ферма и называли его «королем среди любителей». Главный интерес он проявлял к теории чисел, которая в начале 17 столетия стала очень популярной во Франции благодаря новым изданиям трудов древнегреческих математиков. Изучая их, Ферма смог обосновать основные проблемы решения многочисленных задач, которые стали основными для развития классической теории чисел.

Больше всего влияния на Пьера Ферма оказала книга «Арифметика», изучая которую он исписывал поля собственными рассуждениями, впоследствии изменившими развитие математического мышления. В этой книге греческий математик и отец алгебры Диофант Александрийский описывал натуральные числа Пифагора. На основании «Арифметики» Ферма, решая задачи сложных уравнений с несколькими неизвестными, сформулировал легендарное утверждение, позже названное в его честь Великой теоремой Ферма. Доказательство теоремы заняло около 380 лет.

Наибольший научный вклад Ферма в развитие математики в том, что он обратил внимание на роль, которую занимают простые числа

Доказательства с использованием теории групп

Стандартное доказательство

Это доказательство требует самых основных элементов теории групп .

Идея состоит в том, чтобы распознать, что множество G = {1, 2,…, p — 1 } с помощью операции умножения (взятого по модулю p ) образует группу . Единственная групповая аксиома, требующая некоторых усилий для проверки, — это то, что каждый элемент группы G обратим. Принимая это на веру в настоящий момент, давайте предположим , что находится в диапазоне от 1 ≤ ≤ р — 1 , то есть элемент G . Пусть к быть порядка из , то есть, к есть наименьшее целое положительное число такое , что к ≡ 1 ( по модулю р ) . Тогда число 1, , 2 , …, к -1 уменьшаются по модулю р образует подгруппу из G , чей порядок является к и , следовательно, по теореме Лагранжа , K делит порядок G , который является р — 1 . Итак, p — 1 = km для некоторого положительного целого числа m, а затем

ап-1≡аkм≡(аk)м≡1м≡1(модп).{\ Displaystyle а ^ {п-1} \ эквив а ^ {км} \ эквив (а ^ {к}) ^ {м} \ экв 1 ^ {м} \ эквив 1 {\ pmod {p}}.}

Чтобы доказать, что каждый элемент b группы G обратим, мы можем поступить следующим образом. Во- первых, б является взаимно просты с р . Таким образом, тождество Безу гарантирует нам, что существуют целые числа x и y такие, что bx + py = 1 . Читая это равенство по модулю p , мы видим, что x является обратным для b , поскольку bx ≡ 1 (mod p ) . Следовательно, каждый элемент группы G обратим. Итак, как отмечалось ранее, G — группа.

Например, когда p = 11 , инверсии каждого элемента задаются следующим образом:

а	1	2	3	4	5	6	7	8	9	10
а −1	1	6	4	3	9	2	8	7	5	10

Доказательство Эйлера

Если мы возьмем предыдущее доказательство и вместо использования теоремы Лагранжа попытаемся доказать его в этой конкретной ситуации, то мы получим третье доказательство Эйлера, которое он счел более естественным. Пусть A — множество, элементами которого являются числа 1, a , a 2 , …, a k — 1, приведенные по модулю p . Если A = G , то k = p — 1 и, следовательно, k делит p −1 . В противном случае, есть некоторые б ₁ ∈ G \ .

Пусть A ₁ будет множеством, элементами которого являются числа b ₁ , ab ₁ , a 2 b ₁ ,…, a k — 1 b _1, приведенные по модулю p . Тогда A ₁ имеет k различных элементов, поскольку в противном случае было бы два различных числа m , n ∈ {0, 1, …, k — 1 }, таких что a m b ₁ ≡ a n b ₁ (mod p ) , что невозможно, так как из этого следует, что a m ≡ a n (mod p ) . С другой стороны, никакой элемент A _{1 не} может быть элементом A , потому что в противном случае были бы числа m , n ∈ {0, 1,…, k — 1 } такие, что a m b ₁ ≡ a n (mod p ) , а затем б ₁ ≡ п к — м ≡ п + к — м ( по модулю р ) , что невозможно, так как б ₁ ∉ A .

Итак, множество A ∪ A ₁ состоит из 2 k элементов. Если он оказывается равным G , то 2 k = p −1 и, следовательно, k делит p −1 . В противном случае существует некоторый b ₂ ∈ G \ ( A ∪ A ₁ ), и мы можем начать все сначала, определяя A ₂ как множество, элементами которого являются числа b ₂ , ab ₂ , a 2 b ₂ , …, a k — 1 b ₂ приведено по модулю p . Поскольку G конечна, этот процесс должен остановиться в какой-то момент, и это доказывает, что k делит p — 1 .

Например, если a = 5 и p = 13 , то, поскольку

5 2 = 25 ≡ 12 (мод 13) ,
5 3 = 125 ≡ 8 (мод 13) ,
5 4 = 625 1 (мод 13) ,

имеем k = 4 и A = {1, 5, 8, 12 }. Ясно, что A ≠ G = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 }. Пусть b ₁ — элемент группы G \ A ; например, возьмем b ₁ = 2 . Тогда, поскольку

2 × 1 = 2 ,
2 × 5 = 10 ,
2 × 8 = 16 ≡ 3 (мод 13) ,
2 × 12 = 24 ≡ 11 (мод 13) ,

имеем A ₁ = {2, 3, 10, 11 }. Очевидно, что ∪ ₁ ≠ G . Пусть b ₂ — элемент группы G \ ( A ∪ A ₁ ) ; например, возьмем b ₂ = 4 . Тогда, поскольку

4 × 1 = 4 ,
4 × 5 = 20 7 (мод 13) ,
4 × 8 = 32 ≡ 6 (мод 13) ,
4 × 12 = 48 ≡ 9 (мод 13) ,

имеем A ₂ = {4, 6, 7, 9 }. И теперь G = A ∪ A ₁ ∪ A ₂ .

Обратите внимание , что множества A , A 1 , и так далее, на самом деле смежности из А в G .

Целые числа по модулю n

Множество всех целых чисел для модуля п называется кольцо целых чисел по модулю п , и обозначается , или . Однако это обозначение не рекомендуется, поскольку его можно спутать с набором . Кольцо является фундаментальным для различных разделов математики (см. ниже).
ZпZ{\ textstyle \ mathbb {Z} / п \ mathbb {Z}}Zп{\ displaystyle \ mathbb {Z} / n}Zп{\ Displaystyle \ mathbb {Z} _ {п}}Zп{\ Displaystyle \ mathbb {Z} _ {п}}ZпZ{\ Displaystyle \ mathbb {Z} / п \ mathbb {Z}}

Набор определяется для n > 0 как:

ZпZзнак равно{а¯п∣а∈Z}знак равно{¯п,1¯п,2¯п,…,п-1¯п}.{\ displaystyle \ mathbb {Z} / n \ mathbb {Z} = \ left \ {{\ overline {a}} _ {n} \ mid a \ in \ mathbb {Z} \ right \} = \ left \ { {\ overline {0}} _ {n}, {\ overline {1}} _ {n}, {\ overline {2}} _ {n}, \ ldots, {\ overline {n {-} 1}} _ {n} \ right \}.}

(При п = 0 , не является пустым множеством , а, скорее, она изоморфна к , так как = { } .)
ZпZ{\ Displaystyle \ mathbb {Z} / п \ mathbb {Z}}Z{\ Displaystyle \ mathbb {Z}}

Мы определяем сложение, вычитание и умножение по следующим правилам:
ZпZ{\ Displaystyle \ mathbb {Z} / п \ mathbb {Z}}

а¯п+б¯пзнак равно(а+б)¯п{\ displaystyle {\ overline {a}} _ {n} + {\ overline {b}} _ {n} = {\ overline {(a + b)}} _ {n}}
а¯п-б¯пзнак равно(а-б)¯п{\ displaystyle {\ overline {a}} _ {n} — {\ overline {b}} _ {n} = {\ overline {(ab)}} _ {n}}
а¯пб¯пзнак равно(аб)¯п.{\ displaystyle {\ overline {a}} _ {n} {\ overline {b}} _ {n} = {\ overline {(ab)}} _ {n}.}

Для проверки правильности этого определения используются свойства, приведенные ранее.

Таким образом, становится коммутативным кольцом . Например, в кольце мы имеем
ZпZ{\ Displaystyle \ mathbb {Z} / п \ mathbb {Z}}Z24Z{\ Displaystyle \ mathbb {Z} / 24 \ mathbb {Z}}

12¯24+21 год¯24знак равно33¯24знак равно9¯24{\ displaystyle {\ overline {12}} _ {24} + {\ overline {21}} _ {24} = {\ overline {33}} _ {24} = {\ overline {9}} _ {24} }

как в арифметике для 24-часовых часов.

Мы используем обозначения , потому что это фактор — кольцо из по идеалу , набор , содержащий все целые числа , делящиеся на п , где является одноточечное множество {0} . Таким образом , это поле , когда это максимальный идеал (то есть, когда п простой).
ZпZ{\ Displaystyle \ mathbb {Z} / п \ mathbb {Z}}Z{\ Displaystyle \ mathbb {Z}} пZ{\ Displaystyle п \ mathbb {Z}}Z{\ displaystyle 0 \ mathbb {Z}} ZпZ{\ Displaystyle \ mathbb {Z} / п \ mathbb {Z}}пZ{\ Displaystyle п \ mathbb {Z}}

Это также может быть построено из группы только с помощью операции сложения. Класс вычетов a _n — это смежный класс группы a в фактор-группе , циклической группе .
Z{\ Displaystyle \ mathbb {Z}} ZпZ{\ Displaystyle \ mathbb {Z} / п \ mathbb {Z}}

Вместо исключения особого случая n = 0 более полезно включить (который, как упоминалось ранее, изоморфен кольцу целых чисел). На самом деле, это включение полезно при обсуждении характеристики в виде кольца .
ZZ{\ Displaystyle \ mathbb {Z} / 0 \ mathbb {Z}}Z{\ Displaystyle \ mathbb {Z}}

Кольцо целых чисел по модулю п является конечным полем тогда и только тогда , когда п является простым (это гарантирует , что каждый ненулевой элемент имеет мультипликативную обратный ). Если — степень простого числа с k > 1, существует единственное (с точностью до изоморфизма) конечное поле с n элементами, но это не так , которое не может быть полем, потому что оно имеет делители нуля .
пзнак равнопk{\ Displaystyle п = р ^ {к}}граммF(п)знак равноFп{\ Displaystyle \ mathrm {GF} (п) = \ mathbb {F} _ {п}} ZпZ{\ Displaystyle \ mathbb {Z} / п \ mathbb {Z}}

Мультипликативная подгруппа целых чисел по модулю п обозначается . Он состоит из (где a взаимно просто с n ), которые являются в точности классами, обладающими мультипликативным обратным. Это образует коммутативную группу относительно умножения с порядком .
(ZпZ)×{\ Displaystyle (\ mathbb {Z} / п \ mathbb {Z}) ^ {\ times}}а¯п{\ displaystyle {\ overline {a}} _ {n}} φ(п){\ Displaystyle \ varphi (п)}

Эффективный с точки зрения памяти метод

Уменьшение числа требует дополнительных операций модульного сокращения, но уменьшенный размер ускоряет каждую операцию, экономя время (а также память) в целом.

Этот алгоритм использует идентичность

( a ⋅ b ) mod m = [( a mod m ) ⋅ ( b mod m )] mod m

Модифицированный алгоритм:

Положим c = 1 , e ′ = 0 .
Увеличьте e ′ на 1.
Установите c = (b ⋅ c) mod m .
Если e ′ < e , переходите к шагу 2. В противном случае c содержит правильное решение c ≡ b e (mod m ) .

Обратите внимание, что при каждом проходе через шаг 3 выполняется равенство c ≡ b e ′ (mod m ). Если шаг 3 был выполнен e раз, то c будет содержать искомый ответ

Таким образом, этот алгоритм в основном считает e ′ на единицы, пока e ′ не достигнет e , выполняя умножение на b и операцию по модулю каждый раз, когда он добавляет единицу (чтобы гарантировать, что результаты остаются небольшими).

Снова представлен пример b = 4 , e = 13 и m = 497 . Алгоритм проходит шаг 3 тринадцать раз:

e ′ = 1. c = (1 ⋅ 4) mod 497 = 4 mod 497 = 4 .
e ′ = 2. c = (4 ⋅ 4) mod 497 = 16 mod 497 = 16 .
e ′ = 3. c = (16 ⋅ 4) mod 497 = 64 mod 497 = 64 .
e ′ = 4. c = (64 ⋅ 4) mod 497 = 256 mod 497 = 256 .
e ′ = 5. c = (256 4) mod 497 = 1024 mod 497 = 30 .
e ′ = 6. c = (30 4) mod 497 = 120 mod 497 = 120 .
e ′ = 7. c = (120 4) mod 497 = 480 mod 497 = 480 .
e ′ = 8. c = (480 4) mod 497 = 1920 mod 497 = 429 .
e ′ = 9. c = (429 4) mod 497 = 1716 mod 497 = 225 .
e ′ = 10. c = (225 4) mod 497 = 900 mod 497 = 403 .
e ′ = 11. c = (403 4) mod 497 = 1612 mod 497 = 121 .
e ′ = 12. c = (121 4) mod 497 = 484 mod 497 = 484 .
e ′ = 13. c = (484 ⋅ 4) mod 497 = 1936 mod 497 = 445 .

Таким образом, окончательный ответ для c — 445, как и в первом методе.

Как и в первом методе, для этого требуется O ( e ) умножений. Однако, поскольку числа, используемые в этих вычислениях, намного меньше, чем числа, используемые в вычислениях первого алгоритма, время вычислений уменьшается по крайней мере в O ( e ) в этом методе.

В псевдокоде этот метод может быть выполнен следующим образом:

function modular_pow(base, exponent, modulus) is
    if modulus = 1 then
        return 0
    c := 1
    for e_prime = 0 to exponent-1 do
        c := (c * base) mod modulus
    return c

Вычисление

Расширенный алгоритм Евклида

Модульный мультипликативный обратный к модулю м можно найти с помощью расширенного алгоритма Евклида.

Алгоритм Евклида определяет наибольший общий делитель (GCD) двух целых чисел, скажем , и т . Если a имеет мультипликативный обратный по модулю m , этот НОД должен быть 1. Последнее из нескольких уравнений, созданных алгоритмом, может быть решено для этого НОД. Затем, используя метод под названием «обратная подстановка», можно получить выражение, связывающее исходные параметры и этот НОД. Другими словами, можно найти целые числа x и y, удовлетворяющие тождеству Безу ,

а Икс + м у знак равно gcd ( а , м ) знак равно 1. {\ displaystyle ax + my = \ gcd (a, m) = 1.}

Переписанный, это

а Икс — 1 знак равно ( — у ) м , {\ displaystyle ax-1 = (- y) м,}

это,

а Икс ≡ 1 ( мод м ) , {\ Displaystyle Ax \ Equiv 1 {\ pmod {m}},}

Итак, была вычислена модульная мультипликативная обратная к a . Более эффективной версией алгоритма является расширенный алгоритм Евклида, который с помощью вспомогательных уравнений сокращает два прохода алгоритма (обратная подстановка может рассматриваться как прохождение алгоритма в обратном направлении) до одного.

В нотации большого O этот алгоритм работает за время O (log ( m ) 2 ) , предполагая, что | а | < m , и считается очень быстрым и обычно более эффективным, чем его альтернатива, возведение в степень.

Используя теорему Эйлера

В качестве альтернативы расширенному алгоритму Евклида теорема Эйлера может использоваться для вычисления модульных обратных.

Согласно теореме Эйлера , если является взаимно просты с т , то есть, НОД ( , м ) = 1 , то

а ϕ ( м ) ≡ 1 ( мод м ) , {\ Displaystyle а ^ {\ фи (м)} \ экви 1 {\ pmod {м}},}

где — функция Эйлера . Это следует из того факта , что принадлежит мультипликативной группе × тогда и только тогда , когда является взаимно просты в м . Следовательно, модульное мультипликативное обратное можно найти напрямую:
ϕ {\ displaystyle \ phi} ( Z м Z ) {\ Displaystyle (\ mathbb {Z} / м \ mathbb {Z})}

а ϕ ( м ) — 1 ≡ а — 1 ( мод м ) . {\ displaystyle a ^ {\ phi (m) -1} \ Equiv a ^ {- 1} {\ pmod {m}}.}

В частном случае, когда m — простое число, а модульный обратный равен
ϕ ( м ) знак равно м — 1 {\ Displaystyle \ фи (м) = м-1}

а — 1 ≡ а м — 2 ( мод м ) . {\ displaystyle a ^ {- 1} \ Equiv a ^ {m-2} {\ pmod {m}}.}

Этот метод обычно медленнее, чем расширенный алгоритм Евклида, но иногда используется, когда реализация для модульного возведения в степень уже доступна. К недостаткам этого метода можно отнести:

Значение должно быть известно и наиболее эффективным известное вычисление требует м «s факторизации . Широко распространено мнение, что факторизация является сложной вычислительной проблемой. Однако вычисление несложно, когда известно факторизация m на простые множители . ϕ ( м ) {\ Displaystyle \ фи (м)} ϕ ( м ) {\ Displaystyle \ фи (м)}
Относительная стоимость возведения в степень. Хотя это может быть реализовано более эффективно с использованием модульного возведения в степень , при больших значениях m это наиболее эффективно вычисляется с помощью метода редукции Монтгомери . Сам этот алгоритм требует модульного обратного модуля m , который и должен был быть вычислен в первую очередь. Без метода Монтгомери стандартное двоичное возведение в степень , которое требует деления по модулю m на каждом шаге, является медленной операцией, когда m велико.

Одним из заметных преимуществ этого метода является отсутствие условных переходов, зависящих от значения a , и, таким образом, значение a , которое может быть важным секретом в криптографии с открытым ключом , может быть защищено от атак по побочным каналам . По этой причине стандартная реализация Curve25519 использует этот метод для вычисления обратного.

Множественные инверсии

Можно вычислить обратное множество чисел a _i по модулю общего m с помощью одного вызова алгоритма Евклида и трех умножений на каждый дополнительный ввод. Основная идея заключается в формировании произведение всех _я , инвертный , что, затем умножить на виде _J для всех J ≠ я оставить только нужный A −1 _я .

В частности, алгоритм (вся арифметика выполняется по модулю m ):

Вычислите префиксные произведения для всех i ≤ n . б я знак равно ∏ j знак равно 1 я а j знак равно а я б я — 1 {\ textstyle b_ {i} = \ prod _ {j = 1} ^ {i} a_ {j} = a_ {i} b_ {i-1}}
Вычислить b −1 _п используя любой доступный алгоритм.
Для i от n до 2 вычислить
- а −1 _я = b −1 _я b _{i −1} и
- б −1 _{я −1} = b −1 _я а _я .
Наконец, −1 ₁ = b −1 ₁ .

Можно выполнять умножения в древовидной структуре, а не линейно, чтобы использовать параллельные вычисления .

Задания для самопроверки

Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать

Задание 1. Найти значение выражения: 8 * (1 + 6).

Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).

Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).

Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).

Задание 5. Применить распределительный закон умножения: 13 * (3 + + 5 * (4 + 2)

Задание 6. Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним ((20 − 1) * 12 + 30) : 3?

Задание 7. В смартфоне 32 гб памяти. Какое количество приложений можно установить, если одно занимает 1,2 гб?

Задание 8. Верно ли равенство: 8 * 5 = 49?

Ответы

56;
28;
100;
81;
173;
Деление;
26;
Неверно.

Приложения

Приложения китайской теоремы об остатках находятся в диофантовом разделе теории сравнения.

Следующая теорема может рассматриваться либо как приложение китайской теоремы об остатках, либо как обобщение этой теоремы.

Пусть P _i ( x ₁ , x ₂ , …, x _n ) ≡ 0 mod m _i ( i = 1,2, … k) — система из k сравнений, где P _i — многочлены от n переменных , и где модули m _i простые два на два. Тогда эти сравнения совместно платежеспособны тогда и только тогда, когда каждое из них отдельно платежеспособно; более точно, если m является произведением модулей m _i , каждый набор из n ( x ₁ , x ₂ , …, x _n ), где x _i является решением i-го сравнения, биективно определяет n- tuple
( y ₁ , y ₂ , …, y _n ) по модулю m, удовлетворяющий всем сравнениям одновременно.

Более того, если кто-то соглашается называть «примитивным» решение ( x ₁ , x ₂ , …, x _n ) сравнения такое, что каждое из x _i является простым с модулем m _i , то предыдущая теорема остается истина, если мы ограничим его примитивными решениями: сравнения примитивно разрешимы совместно тогда и только тогда, когда каждое из них является отдельно, и существует взаимно однозначное соответствие между наборами примитивных решений по модулю m _i и наборами совместных примитивных решений по модулю m .

Доказательство этой теоремы простое: очевидно, что совместное решение индуцирует решение для каждого уравнения в отдельности, и, наоборот, по таким решениям мы восстанавливаем совместное решение с китайской теоремой об остатках.

Очевидно, что если P _i ( x ) = x — a _i , мы находим китайские теоремы об остатках.

Еще одна пресловутая теорема заключается в следующем:

Пусть P ( x ₁ , x ₂ , …, x _n ) ≡ 0 mod m — сравнение, где P — многочлен от n переменных, и предположим, что m — произведение k модулей m _i, простых двух на два. Тогда это сравнение является растворителем (соответственно изначально растворителем) по модулю m тогда и только тогда, когда оно является растворителем (соответственно примитивно растворителем) по модулю каждого m _i . Опять же, существует взаимно однозначное соответствие между решениями первого сравнения по модулю m и наборами k решений сравнения по модулю каждого m _i . Доказательство аналогично предыдущей теореме.

Благодаря этой последней теореме решение сравнения по модулю m сводится к решению сравнения по модулю каждой из максимальных степеней простых множителей, составляющих m .

Среди множества приложений китайской теоремы об остатках к теории чисел давайте также процитируем доказательство мультипликативности индикатрисы Эйлера .

Родственный метод

Мы видели, что одно из основных приложений китайской теоремы об остатках заключалось в том, что разрешение сравнения по модулю m , произведение двух чисел m ₁ и m ₂ , сводится к разрешению того же сравнения по модулю m _1. и m ₂ , когда m ₁ и m ₂ взаимно просты. Обычно m _i являются степенями простого числа, китайская теорема продвигается настолько далеко, насколько это возможно. Это уже сильно упрощает теоретические и практические задачи, но как уменьшить вопрос еще больше? Следующая техника уже используется Гауссом в Disquisitiones arithmeticae . При умелой практике, чаще всего посредством бесконечного спуска , он позволяет хорошо проанализировать случаи, когда числа m ₁ и m ₂ не являются простыми друг для друга, и, наконец, вернуть вопрос к простым модулям.

Пусть P ( x ₁ , x ₂ , …, x _n ) ≡ 0 mod m — это сравнение, где P — многочлен от n переменных, а m — произведение m ₁ и m ₂ , не обязательно простое между ними. . Разрешение этого сравнения эквивалентно последовательного разрешение от
Р ( х « ₁ , х» ₂ , …, х ‘ _п ) = 0 по модулю т ₁ , то из
Q ( х „ ₁ , х“ ₂ , .. ., x » _n ) ≡ 0 mod m ₂ , где многочлен Q с целыми коэффициентами равен

Q(Икс1,…,Икснет)знак равно1м1п(м1Икс1+Икс1′,…,м1Икснет+Икснет′).{\ displaystyle Q (X_ {1}, \ ldots, X_ {n}) = {1 \ over m_ {1}} P (m_ {1} X_ {1} + x ‘_ {1}, \ ldots, m_ {1} X_ {n} + x ‘_ {n}).}

Демонстрация

Если предложение имеет решение ( x _i ) по модулю m , то это решение, очевидно, является решением по модулю m ₁ . Следовательно, мы можем установить x _i = x ‘ _i + m ₁ x » _i , где ( x’ _i ) — решение предложенного по модулю m ₁ , а x» _i — целое число, определяемое x ‘ _i и x _i . Таким образом, x » _i проверяет, что R ( x» _i ) = 0 mod m , при R = P ( x ‘ _i + m ₁ X _i ) . Но легко видеть, что все коэффициенты многочлена R кратны m ₁ . Поэтому мы можем упростить это последнее сравнение на m ₁ , что дает Q ( x » _i ) = 0 mod m ₂ (обозначения утверждения).

С другой стороны , предположим , что существует решение сравнения Р ( х « _я ) = 0 по модулю т ₁ , а другой конгруэнции Q ( х» _я ) = 0 по модулю м ₂ .
Q определяется из Р и ( х» _я ) , как и раньше . Затем, переходя к предыдущему рассуждению, мы видим, что ( x _i = x ‘ _i + m ₁ x » _i ) является решением предложенного.